- 品牌
- 甘茨
- 服务项目
- 齐全
solve/scalar - 标量情况(单变量和方程)solve/series - 求解含有一般级数的方程solve/system - 解方程组或不等式组第5章 操作表达式5.1 处理表达式Norm - 代数数 (或者函数) 的标准型Power - 惰性幂函数Powmod -带余数的惰性幂函数Primfield - 代数域的原始元素Trace - 求一个代数数或者函数的迹charfcn -表达式和**的特征函数Indets - 找一个表达式的变元invfunc - 函数表的逆powmod - 带余数的幂函数Risidue - 计算一个表达式的代数余combine -表达式合并(对tan,cot不好用)应用:适用于各种数学和科学领域的计算,如物理学、化学、工程学等。黄浦区质量科学计算软件图片
三、科学计算软件的发展趋势随着计算机技术的不断发展,科学计算软件也在不断更新换代。当前,科学计算软件的发展趋势主要呈现以下几个方面:云计算与大数据整合:云计算架构的普及使得科学计算软件能够更加高效地利用计算资源,降低本地硬件的依赖。同时,大数据技术的整合使得软件能够处理更加复杂、庞大的数据集,提高计算的准确性和效率。人工智能与机器学习集成:AI技术的集成使得科学计算软件具备更强的自主决策能力。例如,通过自动化测试、智能推荐等功能,软件能够辅助用户更加高效地完成计算任务。金山区怎样科学计算软件设计在工程设计领域,工程师可以利用软件进行结构分析、流体动力学模拟等,以优化设计方案制造成本。

Maple:用于符号计算和数值计算,适合数学建模和工程应用。Mathematica:强大的计算软件,适用于符号计算、数值计算和可视化。Julia:一种高性能的编程语言,专为科学计算而设计,具有良好的性能和易用性。COMSOL Multiphysics:用于多物理场仿真,适合工程和科学研究。ANSYS:用于工程仿真和有限元分析,广泛应用于机械、土木、航空等领域。SciLab:开源的科学计算软件,功能与MATLAB相似,适合数值计算和可视化。这些软件各有特点,选择合适的工具通常取决于具体的应用需求和个人的使用习惯。
Octave是一种编程语言,旨在解决线性和非线性的数值计算问题。Octave为GNU项目下的开源软件,早期版本为命令行交互方式,4.0.0版本发布基于QT编写的GUI交互界面。Octave语法与Matlab语法非常接近,可以很容易的将matlab程序移植到Octave。同时与C++,QT等接口较Matlab更加方便。Octave是一种科学计算软件,旨在提供与Matlab语法兼容的开放源代码科学计算及数值分析的工具;它同时也是GNU项目成员之一。操作界面。 [1]系统性开发则是由John W. Eaton在1992年接手才开始的。 ***个alpha测试版是在1993年1月4日发布,1.0稳定版则是在1994年2月17日发布。SciLab:开源的科学计算软件,功能与MATLAB相似,适合数值计算和可视化。
开源与协作:开源社区的发展推动了科学计算软件的快速迭代和优化。开发者可以通过共享代码、协作开发等方式,加速技术的创新和应用。跨平台与兼容性:随着IoT设备的普及,科学计算软件需要适应多种终端设备的运行需求。因此,跨平台整合和兼容性成为软件发展的重要方向。四、科学计算软件的影响与挑战科学计算软件的发展对人类社会产生了深远的影响。它不仅提高了科研和工程设计的效率,还推动了教育、金融、医疗等多个领域的创新发展。然而,随着技术的不断进步,科学计算软件也面临着一些挑战。例如,如何保障数据的安全性和隐私性、如何降低软件的复杂性和学习成本、如何适应不断变化的用户需求等。这些问题需要开发者、用户以及相关政策制定者共同努力,以推动科学计算软件的持续健康发展。科学计算软件的应用范围广泛,几乎涵盖了所有需要精确计算的领域。徐汇区定制科学计算软件设计
这些软件通常提供强大的数学库和可视化功能,适用于工程、物理、化学、生物等多个领域。黄浦区质量科学计算软件图片
MatrixMatrixMultiply 计算两个矩阵的乘积MatrixVectorMultiply 计算一个矩阵和一个列向量的乘积VectorMatrixMultiply 计算一个行向量和一个矩阵的乘积MatrixPower 矩阵的幂MinimalPolynomial 构造矩阵的**小多项式Minor 计算矩阵的子式Multiply 矩阵相乘Norm 计算矩阵或向量的p-范数MatrixNorm 计算矩阵的p-范数VectorNorm 计算向量的p-范数Normalize 向量正规化NullSpace 计算矩阵的零度零空间OuterProductMatrix 两个向量的外积Permanent 方阵的不变量Pivot 矩阵元素的主元消去法PopovForm Popov 正规型黄浦区质量科学计算软件图片
甘茨软件科技(上海)有限公司在同行业领域中,一直处在一个不断锐意进取,不断制造创新的市场高度,多年以来致力于发展富有创新价值理念的产品标准,在上海市等地区的数码、电脑中始终保持良好的商业口碑,成绩让我们喜悦,但不会让我们止步,残酷的市场磨炼了我们坚强不屈的意志,和谐温馨的工作环境,富有营养的公司土壤滋养着我们不断开拓创新,勇于进取的无限潜力,甘茨软件供应携手大家一起走向共同辉煌的未来,回首过去,我们不会因为取得了一点点成绩而沾沾自喜,相反的是面对竞争越来越激烈的市场氛围,我们更要明确自己的不足,做好迎接新挑战的准备,要不畏困难,激流勇进,以一个更崭新的精神面貌迎接大家,共同走向辉煌回来!
8.1 操作有理多项式numer,denom - 返回一个表达式的分子/分母frontend - 将一般的表达式处理成一个有理表达式normal - 标准化一个有理表达式convert/parfrac - 转换为部分分数形式convert/rational - 将浮点数转换为接近的有理数ratrecon - 重建有理函数第9章 微积分9.1 取极限Limit, limit - 计算极限limit[dir] - 计算方向极限limit[multi] - 多重方向极限limit[return] - 极限的返回值9.2 连续性测试discont - 寻找一个函数在实数域上的间断点fdiscont -...
- 静安区特色科学计算软件服务电话 2025-09-05
- 普陀区怎样科学计算软件图片 2025-09-05
- 静安区品牌科学计算软件图片 2025-09-04
- 浦东新区智能科学计算软件比较 2025-09-04
- 崇明区怎样科学计算软件供应 2025-09-04
- 闵行区定制科学计算软件推荐 2025-09-04
- 普陀区品牌科学计算软件图片 2025-09-03
- 浦东新区质量科学计算软件供应 2025-09-03
- 虹口区定制科学计算软件设计 2025-09-03
- 嘉定区挑选科学计算软件服务电话 2025-09-03
- 崇明区购买科学计算软件推荐 2025-09-02
- 奉贤区怎样科学计算软件供应 2025-09-02
- 金山区怎样科学计算软件价格 2025-09-02
- 徐汇区定制科学计算软件价格 2025-09-02
- 闵行区智能科学计算软件价格 2025-09-02
- 长宁区定制科学计算软件比较 2025-09-01


- 普陀区常见Matlab服务电话 09-05
- 上海智能Matlab价格 09-05
- 上海挑选Matlab价格 09-05
- 金山区常见科学计算软件比较 09-05
- 松江区品牌Matlab推荐 09-05
- 宝山区质量系统建模软件24小时服务 09-05
- 杨浦区常见Matlab供应 09-05
- 静安区特色科学计算软件服务电话 09-05
- 浦东新区智能系统建模软件供应 09-05
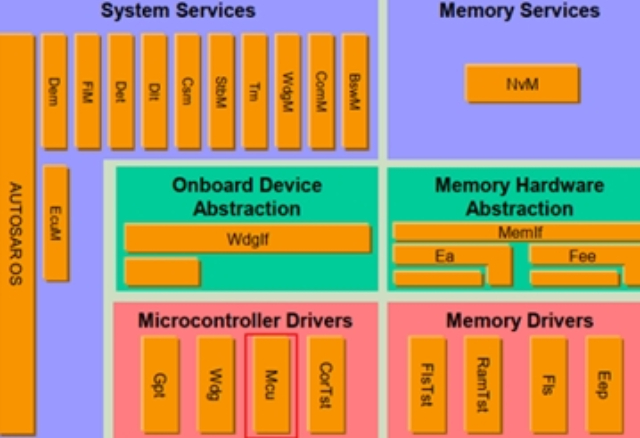
- 金山区品牌AUTOSAR工具链服务电话 09-05